6 bit ÷ ten (decimal)

This is the easiest of the two divisions needed in the spigot algorithm: we have the division of a six bit number (d in the spigot algorithm) by the decimal value ten (i.e. 1010); both quotient and remainder are required.

My solution

Observation: the dividend (A) ranges from 000000 to 111111; 0 through 63 (3F hex), and so, by inspection the quotient (Q) can only take one of seven values: 0, 1, 2, 3, 4, 5 or 6. That is (all numbers decimal): 

A < 10  ⟶ Q = 0

10 ≤ A < 20 ⟶ Q = 1

20 ≤ A < 30 ⟶ Q = 2

30 ≤ A < 40 ⟶ Q = 3

40 ≤ A < 50 ⟶ Q = 4

50 ≤ A < 60 ⟶ Q = 5

60 ≤ A ⟶ Q = 6

So, the game is to determine which of the above ranges the dividend (A) falls into - this immediately gives the quotient, Q. The remainder (R) is then found by multiplying the quotient by ten and subtracting the result from the original dividend (A).

Hence, if 30 ≤ A < 40, we need to subtract 30 (i.e. 011110) from the dividend to get the remainder. And so on, like this:

A < 10  ⟶ Q = 0;    subtract 000000

10 ≤ A < 20 ⟶ Q = 1;    subtract 001010

20 ≤ A < 30 ⟶ Q = 2;    subtract 010100

30 ≤ A < 40 ⟶ Q = 3;    subtract 011110

40 ≤ A < 50 ⟶ Q = 4;    subtract 101000

50 ≤ A < 60 ⟶ Q = 5;    subtract 110010

60 ≤ A ⟶ Q = 6;    subtract 111100

In my first attempt, the above inequalities were determined using 7485 4-bit magnitude comparators (12 off), plus some logic. This seemed an obvious enough approach.

A 74283 4-bit binary full adder dispatches the subtraction of ten times Q from A, giving the remainder, the ten times Q part being realised with some straightforward logic (7427 triple 3-input NOR and 7425 dual 4-input NOR) to decode the Q = 1 through Q = 6 cases into the required subtrahend (e.g. 011110 when Q = 3). This logic actually gives the inverted version of the number to be subtracted (since the 74283 is an adder); the 7404 inverts what's needed for the 3 bits of the quotient Q.  

Here's the circuit:

A refinement

An analysis of the above circuit - which is easy enough to do in Helmut Neemann's Digital logic simulator (i.e. press F9) - gives the following Boolean expressions:

This shows that the twelve 4-bit magnitude comparator solution is a bit of a sledgehammer; the above Boolean expressions can be realised rather more concisely with:

5 off 7420 dual 4-input NAND

3 off 7410 triple 3-input NAND

1 off 74260 dual 5-input NOR

1 off 7411 triple 3-input AND

1 off 7432 quad 2-input OR

1 off 7404 hex inverter

That's a reduction of six chips, plus it's a nicely esoteric selection of 1,2,3,4 and 5 input gates! Note that the 5-input NOR gates are used to implement the 5-input ANDs needed for rows 3 and 4 of the above Boolean expressions, negated versions of the inputs being used to realise the logical AND from the NOR; there isn't a 5-input AND in 74 series TTL. In fact, the 74260 is (I think) the only 5-input gate available in TTL.

Here's the final circuit:

The 7404 hex inverter from the first iteration (needed to invert the 3 bits of quotient Q) has gone; the two 7410 chips each had a spare NAND gate, as did the 7404 chip (used to invert five of the six the bits of the dividend A). The refined approach needs fifteen chips, versus the 22 of the original approach.

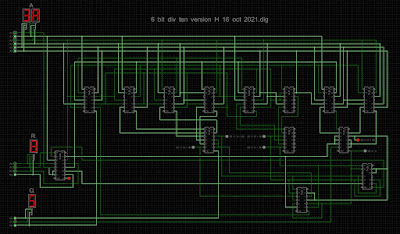
The activated final circuit looks like this:

Here the input (dividend, A) is 3A or 58 decimal; the quotient is 5, and the remainder is 8, the correct answer since 5 × 10 + 8 = 58 (decimal) . The seven LEDs are included for diagnostics: the illuminated LED indicates that 50 ≤ A < 60, which is indeed the case.

Some further examples:

31 ÷ A = 4, remainder 9

3F ÷ A = 6, remainder 3

1E ÷ A = 3, remainder 0

Chip count:

5 × 7420 dual 4-input NAND

3 × 7410 triple 3-input NAND

1 × 74260 dual 5-input NOR

1 × 7411 triple 3-input AND

1 × 7432 quad 2-input OR

1 × 7404 hex inverter

1 × 7427 triple 3-input NOR 

1 × 7425 dual 4-input NOR

1 × 74283 4-bit binary full adder

11 bit × ten multiply

The second multiplication that occurs in the spigot algorithm is that of an eleven bit number (g) by the decimal value ten (i.e. 1010, hex A).

A pragmatic place to start is with the previously described 10 bit × 6 bit multiplier; the six bits of the multiplier being set to 001010, with an eleventh bit added to the multiplicand.

The fact that we are multiplying by a constant (1010) leads to some considerable simplifications; in the first place, all the AND gates can go. The game continues with removing all the circuitry that doesn't do anything. This quickly reduced the thing to just 4 off 74283 4-bit full adder chips.

(One 'trick' that proved useful is to hook up the 11-bit input to an 11-bit counter circuit (3 off 74163 binary counters), and see which lines remain at logic zero (or one), as the counter clocks, and then remove the same.)

In fact, it proves possible to reduce the chip count to just three 74283 chips: after some thought it's apparent that the lower 74283 chip (see circuit below) can do two things: (1) generate bits 12 - 14 of the product, and (2) generate bit P₃ of the product and the carry bit that is needed by what is now the uppermost 74283. We can get away with this because inputs A3 and B3 to the lower 74283 are always zero; whatever happens in the lower part of this adder (i.e. inputs A1, A2, B1, B2) cannot affect the A4, B4 part of the adder (i.e. adder outputs S4 and C4). Cool huh?!

Here's the final 11 bit × ten multiply circuit:

Pressing the space bar activates the circuit in Digital:

Here the input (multiplicand, B) is 7FF or 2047 decimal; the output is 4FF6 or 20470 decimal, the correct answer! The three LEDs, which are the carry outputs from the adders, are included for diagnostics.

Some further examples:

317 × A = 1EE6

754 × A = 4948

001 × A = 000A

007 × A = 0046

In the final circuit, the lowest significant bit of the product (P₀) is connected to ground - it's always zero. The next two bits of the product are also straightforward, given by P₁= B₀ and P₂= B₁. 

This makes sense: since multiplying a number by ten is the same as multiplying the number by 2 and then by 5, it is evident that the lowest significant bit of the product will always be zero; multiplication by 2 being a left shift. The fact that next two bits, P₁ and P₂, are given by B₁ and B₂ is clear from the following example. The right-most three digits of the second row, formed by a shift of the multiplicand (11111111111), have nothing added to them - the row above is zero and the row below is zero; the right-most three digits of the fourth row are also (always) zero, hence the boxed digits appear in the product.

Chip count:

3 × 74283 (4-bit full adder)